Lecture Notes: Relations and Functions

Preliminaries

• Name tags
• Sign in

Course Content

Tuesday Review

Question:

• Draw a Venn diagram illustrating the following information:
  • 10 students are CS majors
  • 8 students are DS majors
  • 2 students are CS/DS double-majors
• Use your Venn diagram to calculate how many students:
  • In total?
  • Are majoring in only CS?
  • Are majoring in only DS?

Answer:

• 16 students total
• 8 students are majoring in only CS
• 6 students are majoring in only DS

Also, write these answers using set notation (e.g., intersection and difference).

Thursday Review

Review Written Assignment 5.

Relations

• A relation is a connection between things.
• For example:
  • Parents and children
  • Pets and their owners
  • Ice cream flavors and their ingredients
  • The numbers greater than x
• Ask: Other examples?
• We will focus on binary relations, which can be represented as ordered pairs.
• Switch to slides
• Slide 1: This table shows a relation between names and addresses
• Names and Addresses can be written as sets
• The relation can be written as a set of ordered pairs.
• This particular relation is a subset of the cross product.
• Each person had one address, and each address was associated with one person. This isn’t true of all relations.
• Slide 2: This relation depicts which courses students are enrolled in.
• Each student is enrolled in four courses.
• Some courses have multiple students enrolled in them.
• We can depict this relation in a diagram
• Draw: Blob diagram. A blob for students and courses. Represent each ordered pair as an arrow.
• We can also describe relations using a rule.
• Write: Birthday Relation: \[ B = \{\langle p, d \rangle : \text{person } p \text{ was born on date } d \} \]
• We could further specify that p is in the set of all people, and d is in the set of all dates.
• Slide 3: This circle represents the set of all points one unit from the origin.
• Write: This can be written as a relation: \[ \{ \langle x, y \rangle : x^2 + y^2 = 1 \} \subseteq \mathbb{R} \times \mathbb{R} \]
• Write: Definition: Given binary relation \( R \subseteq A \times B \), its inverse is: \[ R^{-1} = \{\langle y, x \rangle : \langle x, y \rangle \in R \} \subseteq B \times A \]
• A relation’s inverse simply reverses the order of each pair.
• Draw: Blob diagram, and the inverse of that blob diagram.

Functions

• A function is a special kind of binary relation.
• Write: Definition: A function f from a set A to a set B is a relation \(f \subseteq A \times B\) with the property that for each \(x \in A \), there is one and only one \(y \in B \) such that \(\langle x, y\rangle \in f \).
• If f is a function, a given x uniquely determines a value of y.
• \( y = f(x) \) is the value of f on argument x.
• Mathematical functions are like “pure functions” in programming, always returning the same thing for a given argument.
• Ask: Which of the relations that we’ve seen so far are functions?
  • ✔ Names and Addresses
  • x Enrollments
  • ✔ Birthdays
  • x Circle
• Write: Definition: If \( f \subseteq A \times B \) is a function from A to B, we write \( f : A \rightarrow B \). The set A is called the domain of the function. The set B is called the codomain of the function.
• Ask: What are the domains and codomains of the functions we’ve seen so far?
  • Names and Addresses. Domain: person. Codomain: address.
  • Birthdays. Domain: person. Codomain: birthday.
• In a blob diagram, a function will only have one arrow from each element of the domain.
• Draw: A blob diagram with domain, codomain, f, and arrows.
• Ask: What are the domain and codomain of these mathematical functions?
  • \( f(x) = x^2 \text{ for } x \in \mathbb{Z} \)
  • \( f(n) = n + 1 \)
  • \( f(x) = \frac{1}{x} \)
• The last one is tricky, since the function is undefined for 0.
• We noticed that the enrollment relation was not a function. But if we represent enrollment differently, we can represent it as a function.
• Slide 4: Now, each student is associated with the set of courses in which they are enrolled.
• Write: Let’s call the set of students S and the set of courses C.
• We can specify the domain and codomain of this function as \( e : S \rightarrow \mathcal{P}(C) \)
• For example, \( e(\text{Aisha}) = \{\text{CSCI 121, CSCI 122, MATH 121, SPAN 103}\} \)

Image

• Write: Definition: The value of a function for a given argument is also called the image of that argument.
• That is, \( f(x) \) is the image of \( x \).
• Write: Definition: If A is a subset of the domain of f, then \( f[A] \), the image of the set A, is the set of all images of the elements of A.
• That is, if \( f : S \rightarrow T \) and \( A \subseteq S\), then \[ f[A] = \{ f(x) : x \in A \} \subseteq T \]
• Write: Definition: “A function’s image,” is the image of that function’s domain.
• Draw: X, Y, A, and B. Don’t mention C (the preimage).
  
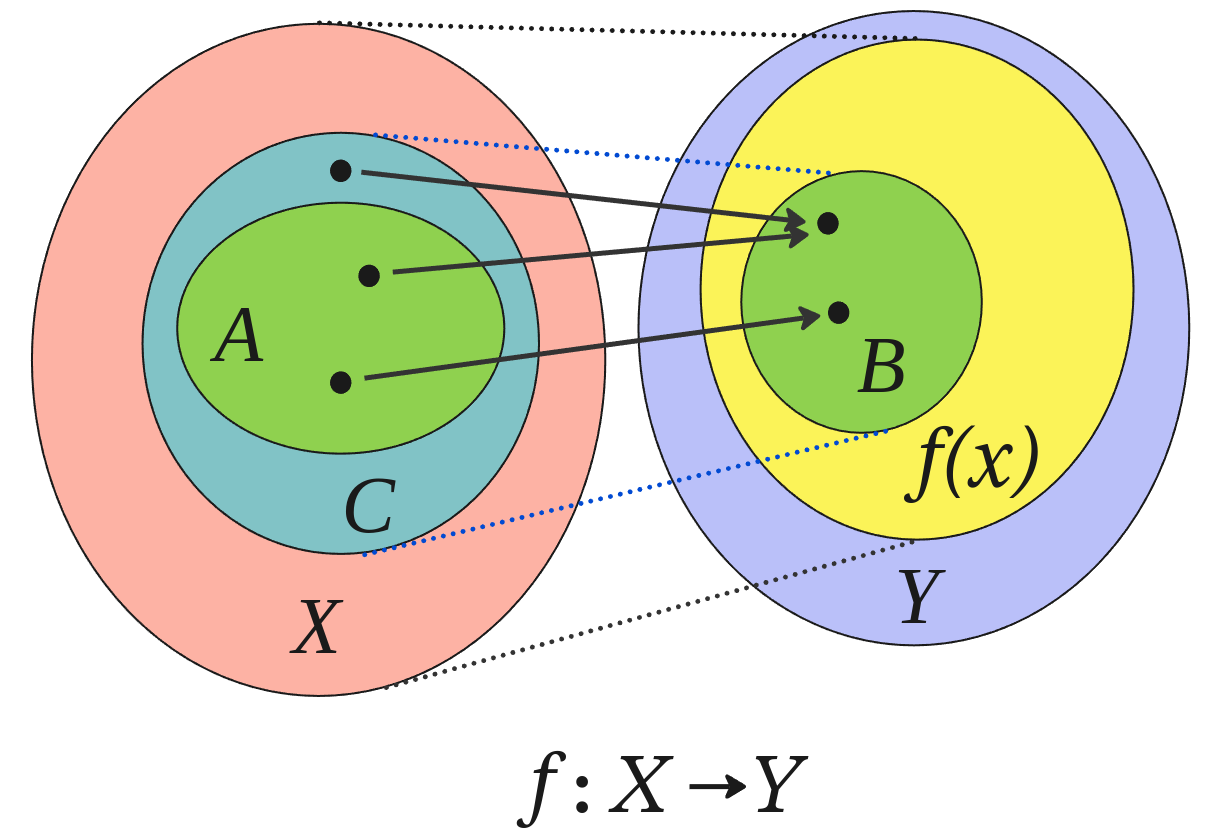
  Credit: Epachamo via Wikipedia.
• Ask: What are the images:
  • \( f(x) = x^2 \text{ for } f : \mathbb{Z} \rightarrow \mathbb{Z}. f[\mathbb{Z}] \)? The set of perfect squares.
  • \(g(x) = 2x \text{ for } f : \mathbb{Z} \rightarrow \mathbb{Z}. g[\mathbb{Z}]\)? The set of even integers. \( g[\mathbb{N}] \)? The set of nonnegative even integers.

Injective

• Write: Definition: An injective function is one for which each element of the codomain is the value of the function for at most one argument. That is, no two different arguments can map to the same value.
• Ask: Are each of these functions injective? When injective, solve by setting \( f(i) = f(j) \) and showing that \( i = j \). When not injective, find a counterexample.
  • ✔ \( f(n) = n + 1 \)
  • x \( B = \{\langle p, d \rangle : \text{person } p \text{ was born on date } d \} \)
  • x \( f(n) = n^2 \text{ for } f : \mathbb{R} \rightarrow \mathbb{R} \)
  • ✔ \( f(n) = n^2 \text{ for } f : \mathbb{N} \rightarrow \mathbb{N} \)
• Draw: Blob diagram. First, make it injective (i.e., at most one arrow ending at each element of B). Then, make it non-injective (i.e., by adding an extra arrow to an element of B).
• An injective function is invertible.
• A function’s inverse is defined the same way as a relation’s inverse. But it can be more clearly expressed using function notation.
• Write: Definition: If \( f : A \rightarrow B \) is injective, then the function \( f^{-1} : f[A] \rightarrow A \), the inverse of f, is defined by the rule that for any \( y \in f[A], f^{-1}(y) \) is that unique element \( x \in A \) such that \( f(x) = y \).
• The inverse has the property that: \[ f(f^{-1}(y)) = y \text{ for any } y \in f[A] \]
• Note that the domain of the inverse need not be all of B, since there may be some unreachable elements in B (i.e., elements of B that are not the value of f for any argument \( x \in A \)).
• Next, let’s find the inverse of \( f(x) = x + 1 \text{ for } f : \mathbb{R} \rightarrow \mathbb{R} \)

• Finally, let’s see that \( f(f^{-1}(y)) = y \text{ for } y = 5 \)

Surjective

• Write: Definition: A function is surjective if every element of the codomain is the value of the function for some argument in the domain. That is, if the image is equal to the codomain.
• \( f : A \rightarrow B \) is surjective if for every \( y \in B \) there is at least one \( x \in A \) such that \( f(x) = y \).
• Ask: Are each of these functions surjective? Find the image for each. Does the image equal the codomain? If not, show a counterexample.
  • ✔ \( f(n) = n + 1 \text{ for } f : \mathbb{R} \rightarrow \mathbb{R} \)
  • ✔ \( B = \{\langle p, d \rangle : \text{person } p \text{ was born on date } d \} \)
  • x \( f(n) = n^2 \text{ for } f : \mathbb{N} \rightarrow \mathbb{N} \)
• Next, let’s consider whether each of these blob diagrams is injective and/or surjective.
• Draw: Each diagram:
  
• Answer: Injective, injective, non-injective, non-injective
• Answer: Non-surjective, surjective, surjective, non-surjective

Bijection

• Write: Definition: A bijection is a function that is both injective and surjective. That is, \( f : A \rightarrow B \) is a bijection if and only if, for every element \( y \in B \), there is one and only one element \( x \in A \) such that \( f(x) = y \).
• In terms of our diagrams, every element of B has exactly one arrow pointing to it.
• Next, let’s label each blob diagram as bijection or not.
• Answer: Not a bijection, a bijection, not a bijection, not a bijection.
• Examples:
  • \( f(n) = n + 1 \text{ for } f : \mathbb{Z} \rightarrow \mathbb{Z} \). This is called the successor function.
  • \( f^{-1} = g(m) = m - 1 \text{ for } g : \mathbb{Z} \rightarrow \mathbb{Z} \). This is called the predecessor function.
  • Both of these functions are bijective: for every integer there is a unique preceding integer and a unique subsequent integer.
  • \( f(x) = 2x \text{ for } f : \mathbb{Z} \rightarrow \mathbb{E} \) where \( \mathbb{E} \) is the set of even integers.
  • This function is also bijective: for every \( y \in \mathbb{E} \), there is one and only one integer \( x \in \mathbb{Z} \) such that \( y = 2x \).
• Recall that: if \( f : A \rightarrow B \) is injective, then we write its inverse as \( f^{-1} : f[A] \rightarrow A \).
• If \( f : A \rightarrow B \) is bijective, then we write its inverse as \( f^{-1} : B \rightarrow A \).
• The inverse of a bijective function is easy to visualize: just reverse the arrows in our blob diagrams.
• Also, note that the inverse of a bijective function will also be bijective.

Functions and Set Cardinality

• Write: Theorem: Finite sets have the same size if and only if there is a bijection between them.
• Proof: If there is a bijection between sets, the sets must have the same size.
• If A and B are finite and f is an injective function from A to B, then \( \vert A \vert \leq \vert B \vert \) since no two different arguments can map to the same value.
• If f is surjective, then \( \vert A \vert \geq \vert B \vert \) since B cannot contain any element that is not the image of an argument in A (i.e., all elements of B must be reachable).
• If f is a bijection (both injective and surjective), then \( \vert A \vert = \vert B \vert \).
• Proof: If sets have the same size, there exists a bijection between the sets.
• Suppose sets A and B have n members each: \[ A = \{ a_1, \ldots, a_n \} \] \[ B = \{ b_1, \ldots, b_n \} \]
• Where if \( i \neq j \text{ and } 1 \leq i, j, \leq n \), then \( a_i \neq a_j \) and \( b_i \neq b_j \).
• Then the function \( f(a_i) = b_i \text{ for } f : A \rightarrow B \text{ for } i = 1, \ldots, n \) is a bijection.
• Write: Definition: Two infinite sets have equal size if and only if there is a bijection between them.
• Given this definition, we can show that not all infinite sets are the same size!
• Since there is a bijection from integers to even integers, the sets are the same size, even though \( \mathbb{E} \subsetneq \mathbb{Z} \).
• There is not a bijection from integers to real numbers, so these sets are not the same size.

Function Composition

• Write: Definition: If \( f : A \rightarrow B, g : C \rightarrow D \) and \( f[A] \subseteq C \), then the function \( g \circ f : A \rightarrow D \) is defined by the rule that \( (g \circ f)(a) = g(f(a)) \) for any \( a \in A \).
• Write: Theorem: Let A, B, and C be any sets. Suppose there exist bijections \( f: A \rightarrow B \) and \( g: A \rightarrow C \). Then there is a bijection \( h : B \rightarrow C \).
• Draw:
  
• We will form a bijection from B to C by following the arrow from B to A, then from A to C.
• Write: Proof: Because f is a bijection, its inverse \( f^{-1} : B \rightarrow A \) exists and is a bijection from B to A.
• Define the function \( h : B \rightarrow C \) as follows: for any \( y \in B, h(y) = g(f^{-1}(y)) \).
• That is, given \( y \in B \), follow the f arrow backwards to find the corresponding element of A, and then follow the g arrow forward to an element of C.
• h is an injection because distinct elements of B correspond to distinct elements of A under \( f^{-1} \), which are mapped by g to distinct elements of C.
• h is a surjection because for any element \( z \in C \), z is the value of h on the argument \( f(g^{-1}(z)) \in B \):
  \(\begin{aligned} h(f(g^{-1}(z))) &= g(f^{-1}(f(g^{-1}(z)))) & \text{ (expand h)} \\ &= g(g^{-1}(z)) & \text{ (f cancels)} \\ &= z & \text{ (g cancels)} \\ \end{aligned}\)
• Since h is an injection and surjection from B to C, h is a bijection from B to C.

Multi-argument Functions (Useful for Lab)

• Functions can accept multiple arguments.
• For example, multiplication is a two-argument function
• Write: Definition: Multiplication is a function \( M : \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z} \) where \( M(m, n) = m \cdot n \) for any \( m, n \in \mathbb{Z} \).
• For example: \( M(3, -5) = 3 \cdot (-5) = -15 \)
• Normally, we write multiplication using infix notation (i.e., the symbol goes between the arguments)
• Writing multiplication as a function uses prefix notation.
• Multi-argument functions can be thought of as single-argument functions where the argument is an ordered tuple.
• For example: \( M(m, n) \) could be written as \( M(\langle m, n \rangle) \).
• Omitting the angle brackets is done for convenience.